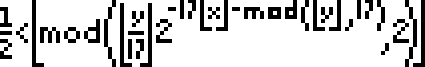So I’m busy today trying to write up a pedagogy paper for Primus outlining a method for teaching calculus students about sequences and series using an extended genetic metaphor. I’ve been teaching it this way for years and I’ve given a couple of mathematical presentations on it, and so it’s about time I had it published.
The basic idea is that an individual function’s Taylor series is akin to an individual person’s DNA molecule: both identify the individual uniquely through a long sequence of values; both can approximate key features with a long enough section to work with; both can be passed on from on individual to its “offspring,” and so on.
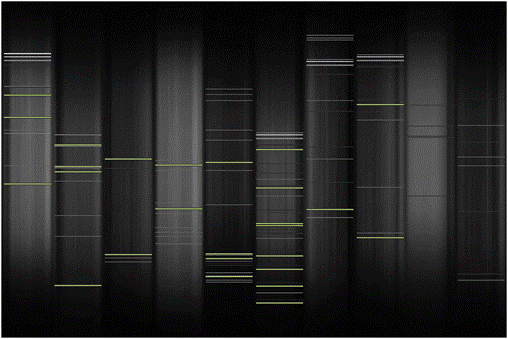
In the process of writing the paper, I wanted to look up some information on the actual chemical structure of DNA, so I turned to the trusty Internet. After a few minutes searching online for information on DNA, I stumbled across this website, which renders webpages using a genetic representation, which struck me as vaguely cool. Specifically, it uses the HTML code of to create a DNA fingerprint for a website. For example, below is the DNA of komplexify; click on it for its interpretation.
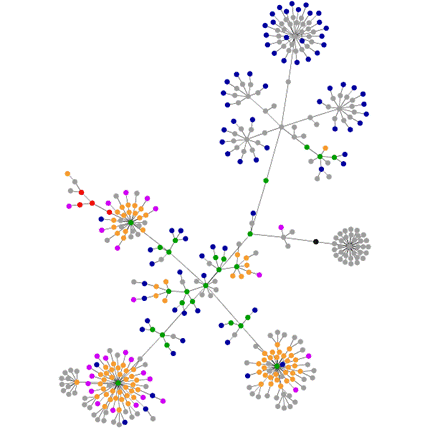
Of course, this has nothing to do with the paper (other than using genetics as a metaphor for something else), but it got me to thinking about other ways to render a website graphically. After a few more minutes searching online, I found this website, which renders websites as connected graphs. For example, below is the graph-theoretical structure of komplexify; click on it for its interpretation.
Now this got me to thinking about other forms of graphical representations, such as the graphical representation of an equation by a curve in the plane. Once upon a time, I remembered reading about an equation whose graph, when plotted in the xy-plane, was precisely the equation used to plot it. After a few more minutes searching online, I found it at Wolfram’s MathWorld site. It’s called Tupper’s Formula, and the graph, which is also the equation (or rather, inequality) that defines it, is below; click on it for the details.
This got me to thinking about the topic of self-reference (a topic we’ve seen here before), and I got to wondering about other completely stand-alone examples of self-reference and, in particular, examples that wouldn’t need a math degree to appreciate. After a few more minutes of online searching, I found this web site, which gives a completely self-referential 20-question multiple-choice exam with a unique solution. In case you’re wondering what the hell such a test could possibly look like, here’s a sample of the questions; click on them to take the test.
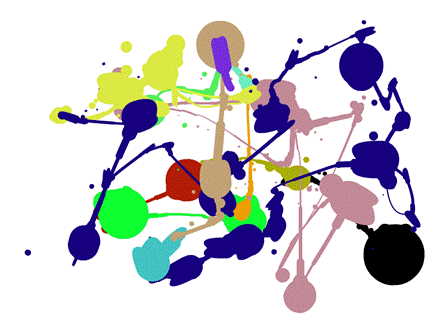
But then that got me surfing the archives linked at the top of the page, which consists of “fresh zero-content for compulsive clickers,” with the hidden caveat that most of the non-content contains some element of mathematical or computer science interest. This got me to thinking about other, more aesthetically-aimed (i.e. less obviously mathematical) zero-content applications for clicking away. After several more minutes of online searching, I found this website, which uses your mouse to create Jackson-Pollack-style digital paintings. Here is one example of my Pollackized mousery; click on it to give it a shot yourself:
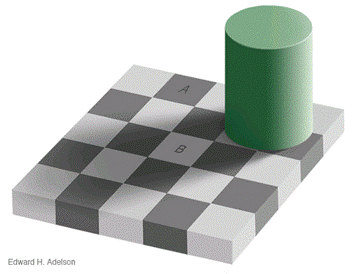
After playing with this for God-knows-how-long, it reminded me of those famous optical illusions wherein a single color appears to be brighter or darker depending on the colors around it. After several more minutes of online searching, I found this website, which features Edward Adelson’s famous iconic example of the Checkboard Illusion — namely, that squares A and B below are the same color — together an explanation of the illusion; click the illusion to get proof!
That got me to thinking about optical illusions in general, which lead me to wonder if there was such a thing as an auditory illusion. After several more minutes of online searching, I found this Wikipedia entry on the Shepard Tone, which is a sound formed by the superposition of sine waves separated by an octave, the upshot of which is that it gives the aural illusion of a tone that forever descends in pitch without ultimately getting any higher or lower. Below is a visual representation of the Shepard tone that you can click to hear.
The concept of forever going downwards without ever changing position reminded me of Escher’s famous Ascending and Descending print. Of course, the Shepard Tone is real, whereas the building in Ascending and Descending is one of Escher’s impossible constructions. That got me to wondering about Escher’s other impossible buildings, and after several minutes of searching online, I was surprised to find this site, which shows how to render Ascending and Descending in the physical world with Legos! It is displayed below; click on it to discover how it was accomplished.
That got me to wondering about what other Escher ideas could be rendered in reality. Another few minutes of searching, and I ended up at this site, based on Escher’s Flatworms. This, shown below, depicts a realistic (though largely impractical) three-dimensional chamber built out of tetrahedral bricks. Click on the work to see how these blocks could be practically engineered in the real world.
But then staring at the undulating columns of the Flatworms world I was reminded of smooth spiral of a helix, which of course reminded me of a double helix, which then reminded me of DNA, which finally reminded me that, despite spending all day on the computer, I had written squat for my paper.
My only solace is the hope that, in relating this sequence of events to you and providing you with all the necessary links, I’ve totally pissed away all the productivity of your day too.